 2 NaOH + H2
2 NaOH + H2
Chemische Reaktionen bilden das Kernstück der Chemie. Sie werden mit dem Ziel angestellt, aus bekannten Stoffen neue Stoffe mit neuen Eigenschaften zu synthetisieren oder unbekannte Stoffe durch typische Reaktionen zu charakterisieren.
Die chemischen Reaktionen können nach verschiedenen Gesichtspunkten eingeteilt werden:
Einteilungskriterium |
Beispiele |
Aggregatzustand |
Feststoffreaktion |
Reaktionsverlauf |
einseitig verlaufend |
Reaktions- |
Hochtemperaturreaktion |
Art des chemischen |
Oxidation |
Reaktionswärme |
exotherm |
Die Darstellung einer Reaktion in einer Reaktionsgleichung ist ein übersichtliches und anschauliches Hilfsmittel, das die an der Reaktion beteiligten Stoffe und deren Umsetzung wiedergibt und den Reaktionstyp erkennen lässt.
Die Aufstellung von Raktionsgleichungen wird durch zwei Grundgesetze ermöglicht:
Bei einer chemischen Reaktion werden weder Elemente zerstört noch neue gebildet.
Die Gesamtmasse der an einer chemischen Reaktion beteiligten Stoffe bleibt unverändert.
Die Edukte (Ausgangsstoffe) stehen auf der linken, die Produkte auf der rechten Seite der Reaktionsgleichung. Dazwischen steht ein Reaktionszeichen, das die Richtung der Reaktion und die Stoff- und Massengleichheit wiedergeben soll.
Durch einen einfachen Pfeil kennzeichnet man Reaktionen, die nur in einer Richtung ablaufen.
2 Na + 2 H2O  2 NaOH + H2
2 NaOH + H2
Gleichgewichtsreaktionen erhalten einen Doppelpfeil, der andeuten soll, dass die Reaktion auf beide Seiten ablaufen kann.
CaCO3 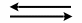 CaO + CO2
CaO + CO2
Besondere Bedingungen werden über den Reaktionspfeil geschrieben.
2 KClO3  2 KCl + 3 O2
2 KCl + 3 O2
Zur leichten Erkennung von entweichenden Gasen oder ausfallenden Niederschlägen setzt man besondere Pfeile ein.
2 Na + 2 H2O  2 NaOH + H2
2 NaOH + H2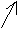
Ca(OH)2 + CO2  CaCO3 + H2O
CaCO3 + H2O
![]()
Die an einer Reaktion beteiligten Edukte und Produkte und deren formelmässige Zusammensetzung müssen bekannt sein.
Kaliumhydroxid KOH reagiert in wässriger Lösung mit Aluminiumchlorid AlCl3 zu Kaliumchlorid KCl und einem Niederschlag von Aluminiumhydroxid Al(OH)3.
Zunächst schreibt man die Formeln der Edukte auf die linke, die der Produkte auf die rechte Seite des Reaktionspfeils. Damit die Stoffbilanz ausgeglichen ist, muss jede Atomsorte, die in den Edukten auftritt auch in den Produkten enthalten sein.
KOH + AlCl3  KCl + Al(OH)3
KCl + Al(OH)3
Damit auch die Massenbilanz ausgeglichen ist, müssen die einzelnen Formeln der Stoffe in geeigneter Weise mit Koeffizienten vervielfacht werden, bis von jeder Atomsorte auf beiden Seiten des Reaktionspfeiles je gleich viele Atome vorhanden sind.
3 KOH + AlCl3  3 KCl + Al(OH)3
3 KCl + Al(OH)3

Erstellen Sie in den folgenden unvollständigen Reaktionsgleichungen die Massengleichheit.
a) |
2 KClO3 |
b) |
2 Fe(OH)3 |
c) |
N2 + 3 H2 |
d) |
TiF4 + 2 H2SO4 |
e) |
4 NH3 + 5 O2 |
f) |
C3H4O2 + 2 O2 |
g) |
4 NO2 + O2 + 2 H2O |
Nicht immer ist es so einfach, durch Vergleichen und Probieren zur Massengleichheit zu kommen. Für solche Fälle bietet sich ein algebraischer Lösungsweg an.
a) x NaOH + y Br2  u NaBr + v NaBrO3 + w H2O
u NaBr + v NaBrO3 + w H2O
Na: |
x = u + v |
x = 1 |
6 NaOH + 3 Br2  5 NaBr + NaBrO3 + 3 H2O
5 NaBr + NaBrO3 + 3 H2O
b) x H3BO3 + y Na2CO3  u Na2B4O7 + v H2O + w CO2
u Na2B4O7 + v H2O + w CO2
H: |
3x = 2v |
x = 1 |
4 H3BO3 + Na2CO3  Na2B4O7 + 6 H2O + CO2
Na2B4O7 + 6 H2O + CO2
c) x C2H2O4 + y KMnO4 + z H2SO4  p CO2 + q MnSO4 + r K2SO4 + s H2O
p CO2 + q MnSO4 + r K2SO4 + s H2O
O: |
4x + 4y + 4z = |
y = 1; r = 1/2; q = 1 |
5 C2H2O4 + 2 KMnO4 + 3 H2SO4 
10 CO2 + 2 MnSO4 + K2SO4 + 8 H2O
Eine chemische Reaktionsgleichung besitzt einen doppelten Aussageinhalt. Sie macht eine qualitative Aussage und eine quantitative.
Beispiel: C2H4 + 3 O2  2 CO2 + 2 H2O
2 CO2 + 2 H2O
Ethen verbrennt zu Kohlendioxid und Wasser.
1 Molekül Ethen verbrennt mit 3 Molekülen Sauerstoff zu 2 Molekülen Kohlendioxid und 2 Molekülen Wasser.
Die quantitative Aussage einer Reaktionsgleichung bezieht sich also auf die an der Reaktion beteiligten Teilchenzahlen. Für diese Teilchenzahlen N hat man die Grösse der Stoffmenge n eingeführt.
Die Masseinheit der Stoffmenge ist 1 Mol.
1 Mol ist die Stoffmenge, die sovielen Teilchen entspricht, wie es in 12,0 g des Kohlenstoffisotops 12C hat.
Die Stoffmenge 1 Mol entspricht 6,02·1023 Teilchen = Avogadrosche Zahl NA.
Die quantitative Aussage der Gleichung lässt sich somit erweitern auf:
1 Mol Ethen und 3 Mol Sauerstoff ergeben 2 Mol Kohlendioxid und 2 Mol Wasser.
Stoffmengen lassen sich allerdings nicht abzählen. Man kann sie nur wägen. 12 g Kohlenstoff enthalten die Stoffmenge 1 Mol. Die Atommassen von Natrium und Kohlenstoff verhalten sich wie 23 : 12. Also muss die gleiche Stoffmenge 1 mol Natriumatome in 23 g Natrium enthalten sein.
Die Molare Masse ist die Masse eines Mols von einem Stoff. Masseinheit: 1 g/mol.
Die Molare Masse M von Atomen in g/mol entspricht zahlenmässig der relativen Atommasse.
Die Molare Masse von Molekülen erhält man durch Addition der Molaren Massen aller am Molekül beteiligten Atome.
Bei Ionenverbindungen berechnet man die Molare Masse einer sog. "Formeleinheit". Die quantitative Aussage einer Gleichung lässt sich somit zu einer Aussage über die Massenverhältnisse der an der Reaktion beteiligten Stoffe erweitern:
28 g Ethen und 96 g Sauerstoff ergeben 88 g Kohlendioxid und 36 g Wasser.
Die Stoffmengen von Gasen oder Dämpfen werden in der Praxis nur selten durch ihre Masse, sondern öfter durch ihr Volumen angegeben.
Der Zusammenhang zwischen der Stoffmenge eines Gases und seinem Volumen liefert das Molvolumen Vm.
Im Normzustand (0°C und 1,013 bar) beträgt das Molare Volumen Vm,n eines idealen Gases 22,41 L/mol.
Für Gasreaktionen lässt sich aus der Reaktionsgleichung sogar eine volumenmässige quantitative Aussage ableiten:
22,4 L Ethen verbrennen mit 67,2 L Sauerstoff zu 44,8 L Kohlendioxid und 44,8 L Wasserdampf.
1. Wie gross ist die Molare Masse von a) H2O b) NaCl c) H2SO4 ?
a) 2·1g/mol + 16g/mol = 18,0 g/mol
b) 23g/mol + 35,5g/mol = 58,5 g/mol
c) 2·1g/mol + 32,1g/mol + 4·16g/mol = 98,1 g/mol
2. Welche Masse und welches Volumen haben 0,74 mol Ammoniak NH3 ?
0,74mol · 17g/mol = 12,6 g
0,74mol · 22,4L/mol = 16,6 L
3. Welcher Stoffmenge entsprechen a) 25 g H2 b) 1 L O2 ?
a) 25g : 2g/mol = 12,5 mol
b) 1L : 22,4l L/mol = 0,0446 mol
4. Wie viele Moleküle sind enthalten in a) 17,2 g CO2 b) 1 L CO2 ?
a) 44g
6,02·1023
17,2g
x x = 2,35·1023
b) 22,41L
6,02·10 23
1 L
x x = 2,69·1022
5. Wie gross ist die Dichte im Normzustand von a) CO2 b) CH4 ?
a) 44g : 22,4L = 1,96 g/L
b) 16g : 22,4L = 0,714 g/L
6. Wie viele Mol Cl--Ionen werden beim Lösen von 2,5 g CaCl2 freigesetzt ?
2,5g : 111,1g/mol = 0,0225 mol
0,0225mol · 2 = 0,045 mol Cl-
7. Wie gross ist der Massenanteil von Schwefel in a) SO2 b) H2SO4
a) 32,1g : 64,1g = 0,50078 = 50,1 %
b) 32,1g : 98,1g = 0,327217 = 32,7 %
8. Wie gross ist der Massenanteil w(Na2CO3) in Kristallsoda Na2CO3·10H2O ?
106g : 286g = 0,370629 = 37,1 %
Mit Hilfe der obigen quantitativen Beziehungen lassen sich Berechnungen über die Stoffumsätze bei einer chemischen Reaktion anstellen.
Die umgesetzten Massen der Reaktionsteilnehmer verhalten sich zueinander wie ihre Molaren Massen.
3,5 kg Bleichromat PbCrO4 sollen durch Umsetzung von Bleiacetat mit Kaliumbichromat hergestellt werden. Welche Ausgangsmengen sind einzusetzen ?
2 Pb(CH3COO)2 + K2Cr2O7 + H2O  2 PbCrO4 + 2 CH3COOH + 2 CH3COOK
2 PbCrO4 + 2 CH3COOH + 2 CH3COOK
2 · 325,3g + 294,2g
2 · 323,2g
x + y
3,5kg
Die unbekannten Mengen berechnen sich aus folgenden Proportionen:
650,6g : 646,4g = x : 3,5kg x = 3,52 kg Bleiacetat 294,2g : 646,4g = y : 3,5kg y = 1,59 kg Kaliumbi.
| 1. | Wie gross ist der Massenverlust beim Glühen von 3,48 g Calciumcarbonat ?
CaCO3 100,1g : 44g = 3,48g : x x = 1,52967g = 1,53 g |
| 2. | Wie viele Liter Luft (Sauerstoffgehalt = 0,21 L/L) braucht es zur Verbrennung von 1,00 kg Koks (Kohlenstoffgehalt = 0,91 g/g) ?
C + O2 12g : 910g = 22,4L : x x = 1698,666L 1698,666L : 0,21 L/L = 8088,88L = 8089 L Luft |
| 3. | Wie viele g Kaliumchlorat müssen erhitzt werden, damit 10,0 Liter Sauerstoffgas (im Nz) entweichen ?
2 KClO3 67,2L : 10L = 245,2g : x x = 36,4880g = 36,5 g KClO3 |
| 4. | 5,00 g einer verdünnten Schwefelsäure werden mit Bariumchlorid versetzt. Es fallen 1,165 g BaSO4-Niederschlag aus. Wie gross ist der Gehalt der verdünnten Schwefelsäure in g/g ?
H2SO4 + BaCl2 98,1g : 233,4g = x : 1,165g x = 0,489659g 0,489659g : 5,0g = 0,0979318 g/g = 0,0979 g/g |
| 5. | Wie viele g Wasser entstehen bei der Explosion von 1,00 Liter Knallgasgemisch ?
2 H2 + O2 67,2L : 1L = 36g : x x = 0,535714g = 0,536 g H2O |
| 6. | Wie gross ist der Gehalt an Phosphorsäure in g/g, wenn 50 g Diphosphorpentoxid in 300 g Wasser aufgelöst werden ?
P2O5 + 3 H2O 142g : 196 = 50g : x x = 69,01408g 69,01408g : 350g = 0,197183g/g = 0,197 g/g H3PO4 |
| 7. | Calciumcarbid wird durch Wasser in Acetylen und Calciumoxid zersetzt. Wie gross ist der Gehalt des Calciumcarbids in g/g, wenn 1,00 kg davon 310 Liter Acetylen (im Nz) liefert ?
CaC2 + H2O 22,4L : 310L = 64,1 : x x = 887,0982g 887.0982g : 1000g = 0,8870982g/g = 0,887 g/g |
| 8. | 10,0 g einer Mischung von je 50 % CaCO3 und MgCO3 werden mit Salzsäure gekocht. Welches Volumen nimmt das dabei entwickelte CO2 (im Nz) ein ?
CaCO3 + 2 HCl MgCO3 + 2 HCl 100,1g : 5g = 22,4L : x x = 1,118881L 84,3g : 5g = 22,4L : y y = 1,328588L 1,118881L + 1,328588L = 2,447469L = 2,45 L CO2 |
Üblicherweise wird der Gehalt einer Lösung durch das Verhältnis aus Masse oder Volumen der gelösten Substanz und Masse oder Volumen der Lösung ausgedrückt. Für Lösungen, die an chemischen Reaktionen teilnehmen ist es oft zweckmässiger, die Stoffmengenkonzentration c anzugeben.
Unter der Stoffmengenkonzentration c versteht man das Verhältnis aus der Stoffmenge an gelöster Substanz und dem Volumen der Lösung.
Ihre Einheit ist 1 mol/L. Sie wird auch als Molarität M bezeichnet.
34 g Natriumhydroxid NaOH werden in Wasser gelöst und auf 500 mL gestellt. Wie gross ist c(NaOH) ?
34g : 40g/mol = 0,85 mol
0,85mol : 0,5L = 1,7 mol/L
| 1. | Es sollen 500 mL einer 0,400 mol/L Kaliumdihydrogenphosphatlösung hergestellt werden. Wie viele g KH2PO4 müssen abgewogen werden ? 0,5L · 0,4mol/L · 136,1g/mol = 27,22g = 27,2 g |
| 2. | Wie gross ist c(NaCl) einer isotonischen Kochsalzlösung mit einem Gehalt von r*(NaCl) = 9,0 mg/mL ? 9g/L : 58,5g/mol = 0,153846mol/L = 0,154 mol/L |
| 3. | Welchen Gehalt in g/L weist eine Schwefelsäurelösung mit c(H2SO4) = 1,5 mol/L auf ? 1,5mol/L · 98,1g/mol = 147,15g/L = 147 g/L |
| 4. | Wie viele mL einer Lösung mit c(NaCl) = 0,5 mol/L lassen sich aus 250 mg NaCl herstellen ? 0,25g : 58,5g/mol = 0,0004273504mol 0,0004273504mol : 0,5mol/L = 0,008547L = 8,55 mL |
| 5. | Wie viele g Kaliumpermanganat müssen abgewogen werden für 250 mL einer Lösung mit c(KMnO4) = 0,2 mol/L ? 0,2mol/L · 0,25L · 158g/mol = 7,9 g |
| 6. | Wie viele g Natriumsulfat Na2SO4·5H2O mit w(Na2SO4·5H2O) = 94,8 % müssen mit Wasser auf 1,0 L verdünnt werden, um eine Lösung mit c(Na+) = 0,10 mol/L zu erhalten ? ½·0,1mol/L·1L·232,1g/mol = 11,605g 11,605g:0,948g/g = 12,24256g = 12,2 g |
Für den Eintritt einer Reaktion ist Bedingung, dass die kleinsten Teilchen der Reaktionspartner aufgrund der Wärmebewegung zusammenstossen. Der Zusammenstoss muss so heftig erfolgen, dass in den reagierenden Stoffen die alten Bindungen gelöst werden, damit durch den Aufbau von neuen Bindungen andere Stoffe entstehen können. Das setzt allerdings voraus, dass die alten Bindungen schon etwas gelockert waren, d.h. dass eine Reaktionsfähigkeit der Stoffteilchen gegeben war.
Eine chemische Reaktion läuft also umso schneller ab, je mehr erfolgreiche Zusammenstösse pro Zeiteinheit zwischen den kleinsten Teilchen erfolgen.
Als Mass für den zeitlichen Ablauf einer chemischen Reaktion dient uns die Reaktionsgeschwindigkeit v.
Unter der Reaktionsgeschwindigkeit v versteht man das Verhältnis aus der Gehaltsänderung der beteiligten Stoffe und der dazu benötigten Zeit.
Die Gehaltsänderungen der an der Reaktion beteiligten Stoffe sind zueinander proportional. Es spielt deshalb keine Rolle, welchen Stoff man betrachtet. Allgemein wird man immer den Stoff wählen, der sich am leichtesten bestimmen lässt.
Die Reaktionsgeschwindigkeit ist von folgenden Faktoren abhängig:
· |
Ionen treffen sich häufiger, weil sie sich anziehen. |
· |
Moleküle sind oft schwerer und bewegen sich langsamer. |
· |
Grosse Moleküle müssen sich zudem an ihren reaktiven Stellen treffen. |
· |
Eine höhere Temperatur bewirkt eine grössere Teilchengeschwindigkeit und es kommt zu mehr Stössen. |
· |
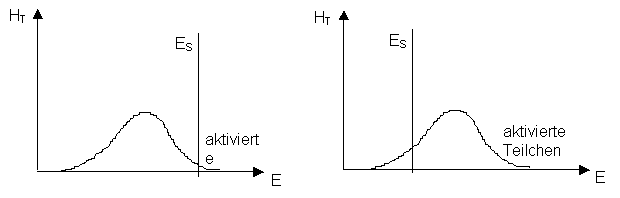
Die Teilchen erhalten zudem eine höhere Energie und der Anteil an erfolgreichen Stössen wird grösser. |
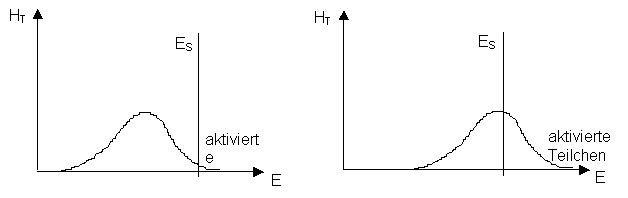
Faustregel: |
Pro 10°C Temperaturerhöhung verdoppelt sich die Reaktionsgeschwindigkeit. |
· |
In heterogenen Systemen können sich die Teilchen der Reaktionspartner nur an der Oberfläche treffen. Je feiner sie also verteilt sind (grosse Oberfläche), umso grösser ist die Reaktionsgeschwindigkeit. |
· |
Reaktionen verlaufen am schnellsten in Lösungen oder in der Dampfphase. |
· |
Katalysatoren sind Stoffe, die in kleinen Mengen die Reaktionsgeschwindigkeit um grosse Beträge vergrössern, indem sie die Energie für einen erfolgreichen Stoss herunter setzen. |
· |
Nach der Reaktion liegen sie in unveränderter Form wieder vor und können erneut in Funktion treten. |
Man unterscheidet die homogene und die heterogene Katalyse.
· |
Katalysator und Reaktionsgemisch sind phasengleich. |
· |
Der Katalysator bildet reaktionsfähige Zwischenverbindungen. |
· |
Katalysator und Reaktionsgemisch bilden verschiedene Phasen. |
· |
Die Reaktionspartner werden an der Katalysatoroberfläche angelagert. Daraus ergibt sich eine hohe Teilchendichte und mehr Stösse. |
· |
Zwischen den angelagerten Teilchen und dem Katalysator finden Wechselwirkungen statt, die die Bindungen lockern. |
· |
Mit der Konzentration ändert sich die Teilchendichte und damit die Wahrscheinlichkeit für Zusammenstösse. |
· |
Die Reaktionsgeschwindigkeit ist proportional zum Produkt der Konzentrationen der Reaktionspartner. v = k · c(A) · c(B) |
k ist eine von allen vorangehenden Faktoren abhängige Proportionalitätskonstante.
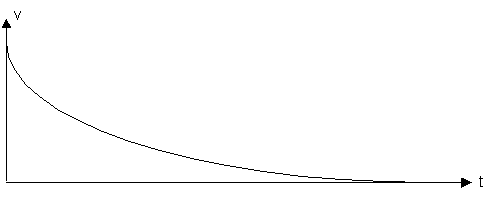
Im Verlaufe einer Reaktion nimmt die Konzentration der Edukte ständig ab und damit auch die Reaktionsgeschwindigkeit.
Viele Reaktionen sind umkehrbar, d.h. die entstandenen Stoffe reagieren miteinander wieder zu den Ausgangsstoffen. Man bezeichnet die beiden Reaktionen als Hin- und Rückreaktion und fasst sie als Gleichgewichtsreaktion zusammen.
A + B 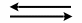 C + D
C + D
Für die Reaktionsgeschwindigkeiten vH und vR gilt:
vH = kH · c(A) · c(B) vR = kR · c(C) · c(D)
Die Rückreaktion verläuft aufgrund der steigenden Konzentrationen der entstandenen Stoffe immer schneller, die Hinreaktion aufgrund der abnehmenden Konzentrationen der Ausangsstoffe immer langsamer. Die Reaktion erreicht einen Zustand, in welchem Hin- und Rückreaktion gleich schnell sind: Die Konzentrationen der Reaktionspartner bleiben konstant, die Reaktion ist scheinbar zum Stillstand gekommen.
Diesen Zustand bezeichnet man als Chemisches Gleichgewicht, entsprechende Reaktionen als Gleichgewichtsreaktionen. Sie verhindern den vollständigen Umsatz der Ausgangsstoffe. Die Gleichgewichtslage wird durch die eingestellten Konzentrationen der beteiligten Stoffe beschrieben.
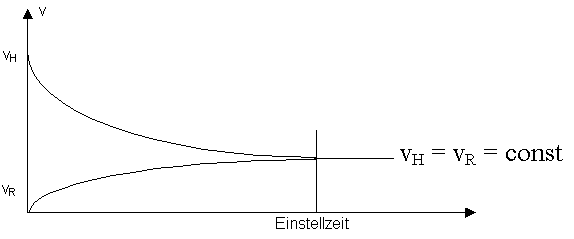
Da im chemischen Gleichgewicht weder vH noch vR Null ist, handelt es sich um ein dynamisches Gleichgewicht.
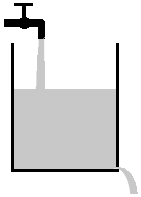 |
Durch den steigenden Flüssigkeitsspiegel steigt der hydrostatische Druck und die Ausfliessgeschwindigkeit. Fliesst gleichviel Wasser aus wie ein, bleibt das Niveau konstant, ein Gleichgewicht hat sich eingestellt. |
Qualitativ lässt sich die Beeinflussung, welche ein Gleichgewicht beim Verändern von Kon-zentrationen, Druck und Temperatur erfährt, mit Hilfe des Prinzips von Le Châtelier beurtei-len.
Wird ein äusserer Zwang auf ein chemisches Gleichgewicht ausgeübt, wird die Teilreaktion begünstigt, die den äusseren Zwang vermindert.
· |
Wärmezufuhr begünstigt die endotherme Teilreaktion. |
· |
Kühlen begünstigt die exotherme Teilreaktion. |
· |
Druckerhöhung begünstigt Teilreaktion mit Volumenabnahme. |
· |
Unterdruck begünstigt Teilreaktion mit Volumenzunahme. |
Beispiel:
Wie beeinflussen eine Temperatur- respektive eine Druckerhöhung die Gleichgewichtslage der folgenden Reaktion ?
2 SO2 + O2 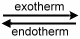 2 SO3
2 SO3
· |
Temperaturerhöhung begünstigt endotherme Reaktion, Gleichgewicht verschiebt sich zugunsten der Edukte. |
· |
Druck begünstigt Hinreaktion wegen Volumenabnahme, Gleichgewicht verschiebt sich zugunsten der Produkte. |
· |
Katalysatoren beeinflussen die Gleichgewichtslage nicht, sie bewirken lediglich eine kürzere Einstellzeit, da sie Hin- und Rückreaktion gleichermassen beschleunigen. |
· |
Wird ein Reaktionspartner aus dem Gleichgewicht entfernt, wird die Teilreaktion begünstigt, die ihn ersetzt. |
· |
Liegt ein Reaktionspartner im Überschuss vor, wird die Teilreaktion begünstigt, die ihn verbraucht. |
Quantitativ wird der Zusammenhang zwischen den Konzentrationen der Reaktionspartner im Chemischen Gleichgewicht durch das Massenwirkungsgesetz ausgedrückt.
Für die Reaktionsgeschwindigkeiten im chemischen Gleichgewicht gilt:
vH = vR
kH · c(A) · c(B) = kR · c(C) · c(D)
Daraus folgt:
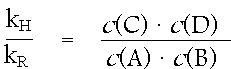
Da sowohl kH wie auch kR bei gegebener Temperatur und gegebenem Druck konstant sind, wird der Quotient kH/kR durch die Gleichgewichtskonstante KC ersetzt.
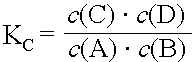
Diese Beziehung wird als Massenwirkungsgesetz bezeichnet. Unter Berücksichtigung der in einer Reaktion auftretenden Koeffizienten wird das MWG wie folgt formuliert:
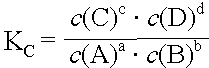
Statt durch die Stoffmengenkonzentrationen kann das MWG auch durch andere, der Stoffmengen- konzentration proportionale Grössen ausgedrückt werden.
Stoffmenge n: |
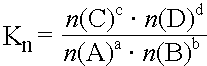 |
Partialdruck p: |
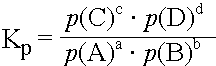 |
Als Satz lässt sich das MWG für eine Reaktion vom Typ A + B 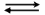 C + D wie folgt formulieren:
C + D wie folgt formulieren:
Für chemische Reaktionen ist im Zustand des Gleichgewichts der Quotient aus dem Produkt der Stoffmengen der Endstoffe und dem Produkt der Stoffmengen der Ausgangsstoffe konstant.
Die Gleichgewichtskonstante K ist ein Mass für die Lage des chemischen Gleichgewichts.
· grosse K-Werte: Gleichgewicht liegt auf der Seite der Produkte.
· kleine K-Werte: Gleichgewicht liegt auf der Seite der Edukte.
Die Gleichgewichtskonstante ist temperatur- und druckabhängig und muss experimentell be-stimmt werden (nachzulesen in Tabellenwerken).
| a) | Für die folgende Reaktion sind die Konzentrationen eines Gleichgewichtsgemisches bei 25°C und 1.013 bar folgende: c(N2O4) = 4,5·10-2 mol/L und c(NO2) = 1,61·10-2 mol/L. Wie gross ist Kc ?
N2O4 Kc = c(NO2)2 : c(N2O4) = (0,0161mol/L)2 : 0,045mol/L = 0,00576 mol/L |
| b) | Für die untenstehende Reaktion ist Kn = 0,771. Wie gross sind die vorliegenden Stoffmengen aller Substanzen im Gleichgewicht, wenn 1 mol H2 und 1 mol CO2 in einem Behälter gemischt werden ?
H2 + CO2 1-x 1-x x x x2 : (1-x)2 = 0,771 x = 0,878 - 0,878x x = 0,468 n(H2O) = n(CO) = 0,468 mol n(H2) = n(CO2) = 0,532 mol |
Ein chemisches Gleichgewicht kann durch Zugabe oder Wegnahme eines Reaktionspartners (Konzentrationsänderung) gestört werden. In der Folge stellt sich ein neues Gleichgewicht ein:
Die Stoffmengen (-konzentrationen) ändern so, dass sich wieder die ursprüngliche Gleichgewichtskonstante ergibt.
Am Beispiel einer Veresterungsreaktion sollen rechnerisch die Möglichkeiten der Veränderung der Konzentrationen und ihre Auswirkung auf die Ausbeute aufgezeigt werden:
Für die Umsetzung von Ethanol mit Ethansäure zu Ethylethanoat und Wasser hat die Gleichgewichtskonstante Kn bei 25°C den Zahlenwert 4.
Zur Veresterung werden 1 mol Ethanol und 1 mol Ethansäure eingesetzt. Welche Ausbeute an Ester kann höchstens erzielt werden ?
C2H5OH + CH3COOH 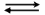 CH3COOC2H5 + H2O
CH3COOC2H5 + H2O
1-x 1-x x x
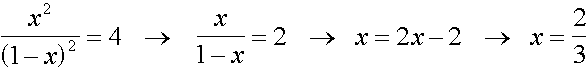
n(CH3COOC2H5) = 0,667 mol  66,7 % Ausbeute
66,7 % Ausbeute
Auf 1 mol Ethanol werden 2 mol Ethansäure angesetzt. Wie gross ist nun die maximale Ausbeute an Ester ?
C2H5OH + CH3COOH 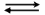 CH3COOC2H5 + H2O
CH3COOC2H5 + H2O
1-x 2-x x x
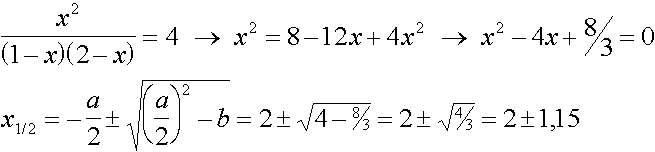
x1 = 3,15 (scheidet aus)
x2 = 0,85  n(Ester) = 0,85 mol
n(Ester) = 0,85 mol  85 % Ausbeute
85 % Ausbeute
Zur Veresterung werden 1 mol Ethanol und 1 mol Ethansäure angesetzt und das entstehende Wasser mit einem wasserbindenden Mittel entzogen, sodass nur noch 8 % des entstehenden Wassers vorliegen. Welche Ausbeute an Ester kann so erzielt werden ?
C2H5OH + CH3COOH 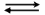 CH3COOC2H5 + H2O
CH3COOC2H5 + H2O
1-x 1-x x 0,08x
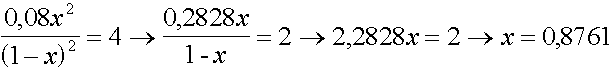
n(Ester) = 0,8761 mol  87,6 % Ausbeute
87,6 % Ausbeute
· |
Durch Erhöhung der Konzentration eines Edukts wird die Ausbeute erhöht. |
· |
Durch Wegnahme eines Produkts kann durch die Nachreaktion eine höhere Ausbeute erzielt werden. |
· |
Wenn Gase entweichen oder Niederschläge ausfallen, reagieren die Edukte vollständig. |
Alle chemischen Reaktionen sind mit Energieumsetzungen verbunden. Dabei kommen im wesentlichen drei Energieformen vor:
Wärmeenergie |
häufigste Energieform bei Reaktionen |
Dabei gilt wie in der Physik das Gesetz von der Erhaltung der Energie:
Der Gesamtbetrag an Energie im abgeschlossenen Reaktionssystem bleibt erhalten.
Ist die innere Energie der Ausgangsstoffe grösser als diejenige der Reaktionsprodukte, liegt die frei werdende Energie meist als Wärme, manchmal auch als Licht- oder elektrische Energie vor. In diesem Falle spricht man von einer exothermen Reaktion.
Im umgekehrten Falle tritt Abkühlung ein. Sehr oft kommt die Reaktion dadurch zum Stillstand und Energie muss in Form von Wärme, Licht oder Elektrizität zugeführt werden. Es liegt eine endotherme Reaktion vor.
Oft laufen chemische Reaktionen nicht ab, ohne dass ihnen vorgängig Energie zugeführt wird. Die Energie wird benötigt, um Bindungen zu lockern und damit die Zusammenstösse zwischen den reagierenden Teilchen genügend heftig sind. Den zuzuführenden Energiebetrag bezeichnet man als Aktivierungsenergie.
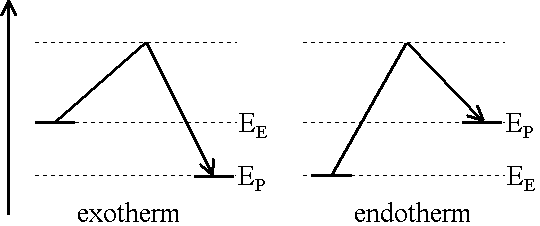
Die Gleichung der exothermen Reaktion S + O2  SO2 ist somit energetisch betrachtet nicht komplett, denn der Energieinhalt (innere Energie) der Ausgangsstoffe ist grösser als derjenige des SO2, weil bei der Reaktion Wärme freigesetzt wird.
SO2 ist somit energetisch betrachtet nicht komplett, denn der Energieinhalt (innere Energie) der Ausgangsstoffe ist grösser als derjenige des SO2, weil bei der Reaktion Wärme freigesetzt wird.
Die Energiebilanz muss eingerichtet werden durch die Anfügung der entstehenden Wärme. Man schreibt die thermochemische Gleichung.
S + O2  SO2 + 296,8 kJ
SO2 + 296,8 kJ
Die Energieangabe bezieht sich auf den stöchiometrischen Ansatz. Sie wird als Reaktionswärme bezeichnet. Das Reaktionssystem wird bei der Angabe der Reaktionswärme von aussen betrachtet. Die Wärme wird bei obiger Reaktion freigesetzt (exotherm) und an die Umgebung abgegeben (positive Reaktionswärme).
Üblicher ist es allerdings, den Beobachtungspunkt in das System zu verlegen. Die umgesetzten Energien erhalten so betrachtet umgekehrte Vorzeichen und werden als Reaktionsenthalpien DH bezeichnet.
exotherm: |
System verliert Energie, Vorzeichen negativ |
endotherm: |
System nimmt Energie auf, Vorzeichen positiv |
Reaktionsenthalpien werden aus der Gleichung herausgenommen und wie folgt geschrieben:
S + O2  SO2 DH = -296,8 kJ
SO2 DH = -296,8 kJ
Reaktionsenthalpien sind temperatur- und druckabhängig. In der Regel werden Tabellenwerte auf 25°C und 1013 mbar bezogen.
Die Reaktionsenthalpie für die Bildung von 1 Mol einer Verbindung aus den Elementen bezeichnet man als Bildungsenthalpie DHB.
H2 + ½ O2  2 H2O DHB = -286,J kJ
2 H2O DHB = -286,J kJ
Die Reaktionsenthalpie ist unabhängig vom Reaktionsweg. Sie ist gleich der Summe der Reaktionsenthalpien der Zwischenstufen. Aus diesem Grunde können Reaktionsenthalpien aus den tabellierten Bildungsenthalpien der Produkte und Edukte bestimmt werden. Die Bildungsenthalpie der Produkte wird dabei freigesetzt, diejenige der Edukte muss aufgewendet werden, um diese vorerst in die Elemente zu zerlegen.
DH = DHB der Produkte - DHB der Edukte
Zu berechnen ist die Verbrennungsenthalpie von C2H5OH aus den Bildungenthalpien von C2H5OH (-278,5 kJ/mol), CO2 (-394,1 kJ/mol) und H2O (-286,3 kJ/mol).
C2H5OH + 3 O2  2 CO2 + 3 H2O
2 CO2 + 3 H2O
DH = 2(-394,1kJ/mol) + 3(-286,3kJ/mol) - (-278,5kJ/mol) =
-1368,6 kJ/mol
Bei einer chemischen Reaktion werden alte Bindungen gelöst und neue gebildet. Ob der Vorgang endotherm oder exotherm verläuft, hängt hauptsächlich davon ab, ob zur Aufspaltung der Bindungen mehr Energie aufgewendet werden muss als die Bildung der neuen Bindungen freisetzt oder ob das Umgekehrte der Fall ist.
Die Energie für die Aufspaltung einer kovalenten Bindung bezeichnet man als Bindungsenergie. Sie ist ein Mass für die Stärke der Bindung und natürlich auch von der chemischen Umgebung abhängig. Durchschnittswerte können entsprechenden Tabellen entnommen werden. Mit ihrer Hilfe lassen sich mit genügender Genauigkeit Voraussagen über die Energiebilanz einer Reaktion machen.
Die Bindungsenergien haben ein positives Vorzeichen. Werden Bindungen gebildet, entspricht die freiwerdende Energie der Bindungsenergie mit negativem Vorzeichen. Die Reaktionsenthalpie enrgibt sich als Summe der aufgewendeten und zurückgewonnenen Energien.
Berechnen Sie mit Hilfe der Bindungsenergien die Reaktionsenthalpie für die folgende Reaktion (alle Reaktionspartner sind gasförmig).
4 NH3 + 3 O2  2 N2 + 6 H2O
2 N2 + 6 H2O
DH = 12·390kJ + 3·494kJ - 2·943kJ - 12·465kJ = -1304 kJ
Frage
Wie lässt sich die zunehmende Bindungsenergie von der Kohlenstoffeinfachbindung zur Dreifachbindung mit der Reaktivität dieser Bindungstypen vereinbaren ?
Der Lösungsvorgang eines Salzes in Wasser lässt sich in drei Schritte gliedern:
1. |
Die Wassermoleküle lagern sich an der Kristalloberfläche an und lockern die Bindungskräfte im Kristall. |
2. |
Aufgrund der Wärmebewegung der Wassermoleküle werden die gelockerten Ionen vom Kristall abgelöst. Dazu muss die Gitterenergie aufgewendet werden. |
3. |
In der Lösung werden die Ionen von Wassermolekülen umhüllt. Dieser Vorgang wird mit Hydratation bezeichnet und ist exotherm (Hydratationswärme). |
Ist die Gitterenergie grösser als die Hydratationswärme, kühlt sich die Lösung ab, andernfalls erwärmt sie sich.
Salz |
Gitterenergie |
Hydratationswärme |
Summe |
Effekt |
KCl |
+ 704 |
- 687 |
+ 17 |
Abkühlung |
KF |
+ 806 |
- 823 |
- 17 |
Erwärmung |
NaNO3 |
+ 673 |
- 653 |
+ 20 |
Abkühlung |
Um die Löslichkeit verschiedener Stoffe vergleichen zu können, verwendet man den Begriff der Löslichkeit:
Die Löslichkeit eines Stoffes gibt an, wie viele g dieses Stoffes bei einer bestimmten Temperatur in 100 g Lösemittel maximal gelöst werden können.
In der Regel nimmt die Löslichkeit eines festen Stoffes bei steigender Temperatur zu, die eines Gases ab (bei konstantem Druck).
Zwischen einer gesättigten, wässrigen Lösung eines schwerlöslichen Salzes und ihrem Bodenkörper stellt sich ein dynamisches Gleichgewicht ein: Es lösen sich pro Zeiteinheit gleich viele Teilchen, wie auskristallisieren.
AB (fest) 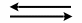 A+ + B-
A+ + B-
Auf dieses Gleichgewicht lässt sich das Massenwirkungsgesetz anwenden:
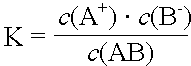
Solange noch ein Bodenkörper des Salzes vorhanden ist, kann die Konzentration des Salzes als konstant betrachtet werden.
K · c(AB) = L(AB) = c(A+) · c(B-)
Das Löslichkeitsprodukt gilt nur für gesättigte Lösungen schwerlöslicher Salze und ist temperaturabhängig. Es wird in seiner allgemeinen Form wie folgt ausgedrückt:
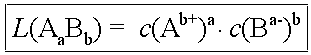
Für die Berechnung des Löslichkeitsproduktes aus der Stoffmengenkonzentration an gelös-tem Salz ergibt sich, unter Berücksichtigung der durch die Stöchiometrischen Koeffizienten bedingt unterschiedlich grossen Ionenkonzentrationen, die folgende Beziehung:
AaBb 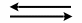 a Ab+ + b Ba-
a Ab+ + b Ba-
L(AaBb) = c(Ab+)a · c(Ba-)b = [a·c(AaBb)]a · [b·c(AaBb)]b
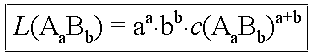
Und umgekehrt für c(AaBb):
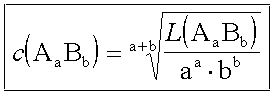
Löslichkeitsprodukte einiger schwerlöslicher Salze bei 20°C:
L(AgCl) |
= |
1,6·10-10 mol2/L2 |
L(AgBr) |
= |
6,3·10-13 mol2/L2 |
L(AgI) |
= |
1,0·10-16 mol2/L2 |
L(Al(OH)3)) |
= |
8,0·10-32 mol4/L4 |
Die Löslichkeit eines Salzs ist von der gleichzeitigen Gegenwart anderer Salze in der Lösung abhängig. Besonders stark ist die Beeinflussung durch solche Salze, die ein gleiches Anion oder Kation enthalten. Das Löslichkeitsprodukt des schwerer löslichen Salzes kann nämlich nicht überschritten werden.
So wird das Kation eines schwerer löslichen Salzes durch Zugabe eines zweiten Salzes mit gleichem Anion soweit ausgefällt, bis sich sein Löslichkeitsprodukt eingestellt hat. Ein zweites Salz mit gleichem Kation fällt umgekehrt das Anion aus.
Von dieser Tatsache macht man in der Gravimetrie Gebrauch, wo ein bestimmtes Ion zur quantitativen Bestimmung möglichst vollständig aus einer Lösung ausgefällt werden soll.
Ein weiteres Anwendungsgebiet ist das Aussalzen eines Stoffes.
| 1. | Berechnen Sie das Löslichkeitsprodukt L(BaSO4), wenn in 1,00 Liter gesättigter Lösung 2,4 mg Bariumsulfat löslich sind. 0,0024g/L:233,4g/mol = 1,028·10-5mol/L L(BaSO4) = c(Ba2+)·c(SO42-) = (1,028·10-5mol/L)2 = 1,06·10-10 mol2/L2 |
| 2. | Wie viele mg AgCl sind in 1 Liter gesättigter Lösung gelöst, wenn L(AgCl) bei 20°C 1,61·10-10 mol2/L2 beträgt ? c(AgCl) = c(Ag+) = c(Cl-) = (1,61·10-10mol2/L2)½ = 1,269·10-5mol/L r*(AgCl) = 1,269·10-5mol/L·143,2g/mol = 1,82 mg/L |
| 3. | Das Löslichkeitsprodukt von Silbercarbonat beträgt bei 25 °C 6,15·10-12 mol3/L3. Welche Massenkonzentration r*(Ag2CO3) in mg/L hat eine gesättigte Silbercarbonatlösung ?
r*(Ag2CO3) = 1,1541·10-4mol/l·275,75g/mol = 0,031824g/L = 31,8 mg/L |
| 4. | Wie gross ist c(Ba2+) in einer gesättigten BaSO4-Lösung ? L(BaSO4) = 10-10 mol2/L2 a) in reinem Wasser b) in 0,10 mol/L Na2SO4-Lösung a) c(Ba2+) = c(SO42-) = (10-10mol2/L2)½ = 10-5 mol/L b) c(Ba2+)·0,1mol/L = 10-10mol2/L2 c(Ba2+) = 10-10mol2/L2:0,1mol/L = 10-9 mol/L |
| 5. | Calciumsulfat hat ein Löslichkeitsprodukt von 6·10-5 mol2/L2. Wie viele g K2SO4 müssen 1 Liter Gipswasser enthalten, wenn c(Ca2+) 0,1 mmol/L sein soll ? L(CaSO4) = 10-4mol/L·c(SO42-) = 6·10-5mol2/L2 c(SO42-) = 6·10-5mol2/L2:10-4mol/L = 0,6mol/L r*(K2SO4) = 0,6mol/L·174,3g/mol = 105 g/L |
| 6. | Mit wie vielen Millilitern Waschflüssigkeit darf eine gravimetrische Fällung von PbSO4 gewaschen werden, damit höchstens 0,3 mg PbSO4 gelöst werden ? L(PbSO4) = 2·10-8 mol2/L2 a) Waschflüssigkeit ist reines Wasser b) Waschflüssigkeit ist 0,1 mol/L H2SO4 a) c(PbSO4) = (2·10-8mol2/L2)½ = 1,4142·10-4mol/L r* = 1,4142·10-4mol/L·303,3g/mol = 0,042893g/L V = 0,3mg:0,042893mg/mL = 6,9941ml = 7,0 mL b) c(PbSO4) = 2·10-8mol2/L2:0,1mol/L = 2·10-7mol/L r* = 2·10-7mol/L·303,3g/mol = 6,06·10-5g/L V = 0,3mg:6,06·10-2mg/L = 4,95049L = 5,0 L |